Dans une trace GPS, il y a bien souvent des outliers, des points qui sont situés loin de la trace momentanément, et qui sont très probablement très imprécis. On remarque bien, sans besoin d’être expert, que ces points ne sont pas normaux. Il est essentiel, dans l’analyse de traces GPS, de pouvoir détecter ces outliers et de supprimer ces points, de sorte à obtenir une trace GPS dont les points restant sont très probablement précis. Il existe pour cela plusieurs moyens (Zheng and Zhou 2011), dont deux très efficaces et rapides : les filtres moyens et médians.
Ici je vais me focaliser sur le filtre médian et montrer comment le mettre en place très simplement, sur R.
Voici ci-dessous une trace GPS, qui ne comporte pas vraiment d’outlier. Peu importe, l’idée ici est de montrer comment mettre en place une trace médiane, qui servira de référence au filtre.
ggplot(points, aes(x = x, y = y)) + geom_path() + theme_void()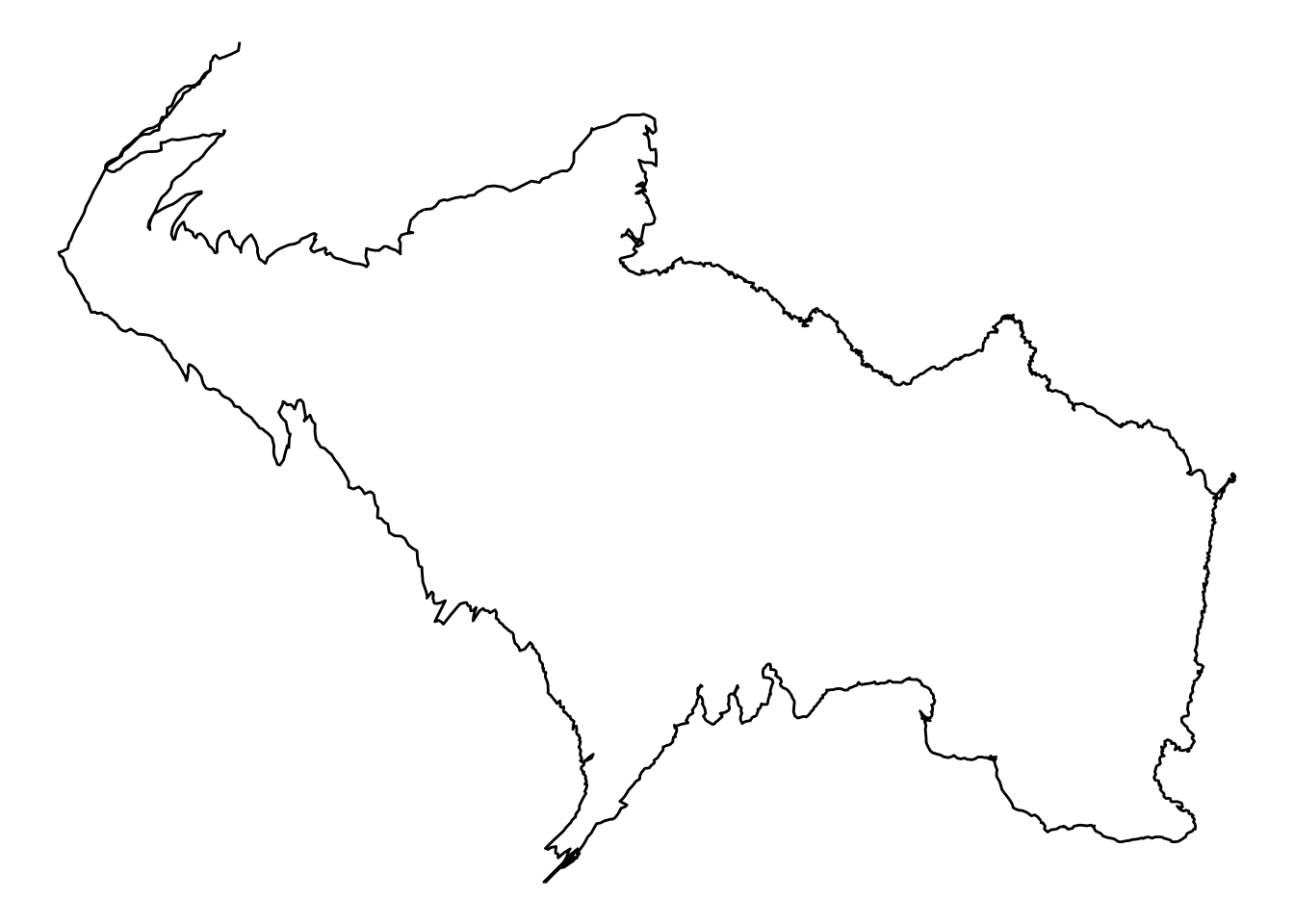
Afin de calculer la trace médiane, je vais appliquer une fenêtre glissante avec un paramètre w (paramètre représentant la largeur de la fenêtre) sur i) les longitudes et ii) les latitudes. Pour cela, je créé une fonction qui prend en entrée les longitudes et latitudes, et en paramètre la largeur de la fenêtre (ainsi que la règle pour les extrémités des données). L’output est, pour un couple de coordonnées GPS, son équivalent médian.
median_smooth = function(x, y, w = 7, endr = "keep"){
xmed = runmed(x, w, endrule = endr)
ymed = runmed(y, w, endrule = endr)
return(cbind(xmed, ymed))
}Appliquons maintenant cette fonction à notre trace GPS, avec un paramètre w équivalent à 7, et visualisons la trace médiane.
points[, c("xmed", "ymed")] = median_smooth(points$x, points$y, w = 7)
ggplot(points, aes(x = xmed, y = ymed)) + geom_path() + theme_void()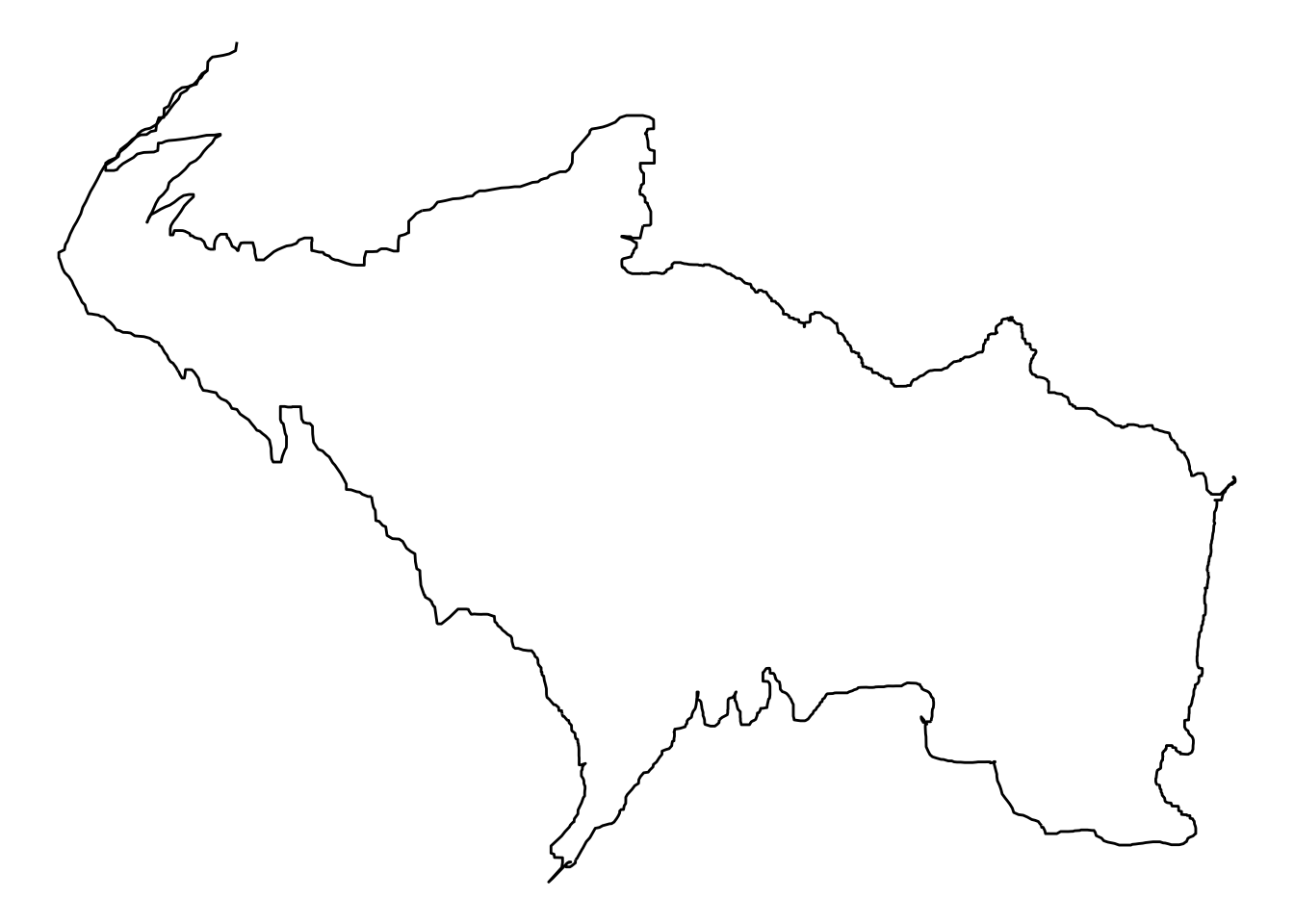
La trace médiane est bien plus lisse, et certains pics ont presque disparus. Essayons encore mais en élargissant la fenêtre, à 11.
points[, c("xmed", "ymed")] = median_smooth(points$x, points$y, w = 11)
ggplot(points, aes(x = xmed, y = ymed)) + geom_path() + theme_void()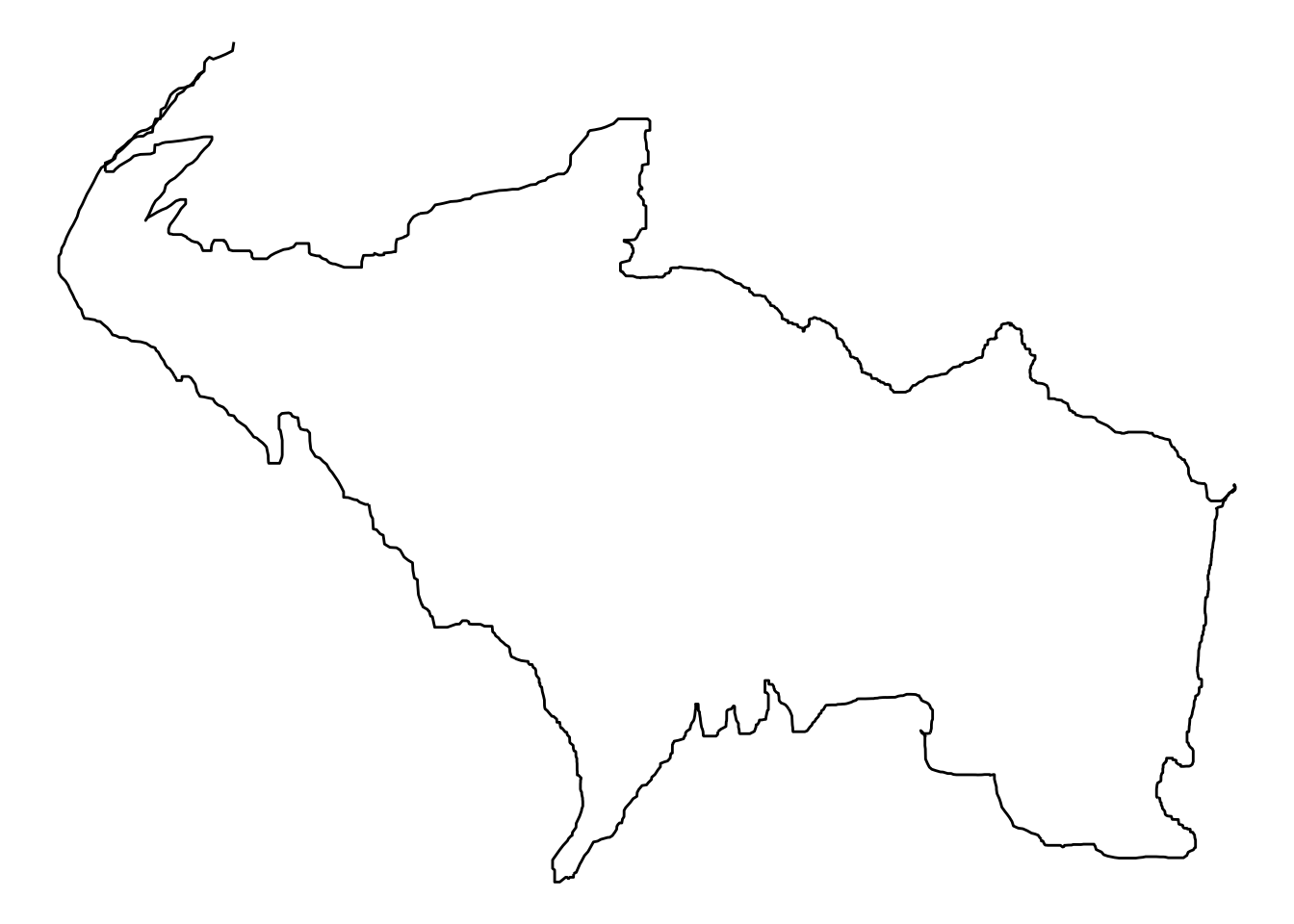
Dans ce cas, certains pics ont complètement disparu, comme celui qui était présent au sud de la trace.
Le but du filtre médian n’est pas de remplacer la trace GPS brute par la trace médiane, mais bien de supprimer, ou d’annoter, les points GPS de la trace brute qui seraient trop éloignés de la trace médiane. Donc, une fois la trace médiane obtenue, il s’agit de calculer la distance des points GPS à la trace médiane (en géométrie points ici, mais peut-être faudrait il une géométrie ligne), puis de déterminer un seuil de distance pour lequel les points GPS seraient considérés comme des outliers. Pour cela, je créé une fonction qui ressemble à la première mais qui, au lieu d’avoir en output une trace médiane, retourne la distance de chaque point GPS à la coordonnée médiane.
median_filter = function(x, y, w = 7, endr = "keep"){
xmed = runmed(x, w, endrule = endr)
ymed = runmed(y, w, endrule = endr)
distmed = unlist(lapply(c(1:length(x)), function(i){round(dist(rbind(cbind(x[i], y[i]), cbind(xmed[i], ymed[i]))),1)}))
return(distmed)
}Appliquons désormais ce filtre à notre trace, et en représentant les points éloignés de 15m ou davantage à la trace médiane en rouge :
points[, "dmed"] = median_filter(points$x, points$y, w = 7)
points$size = NA
points$size[points$dmed >= 15] = 2
ggplot(points, aes(x = x, y = y)) + geom_path() + geom_point(size = points$size, color = 2) + theme_void()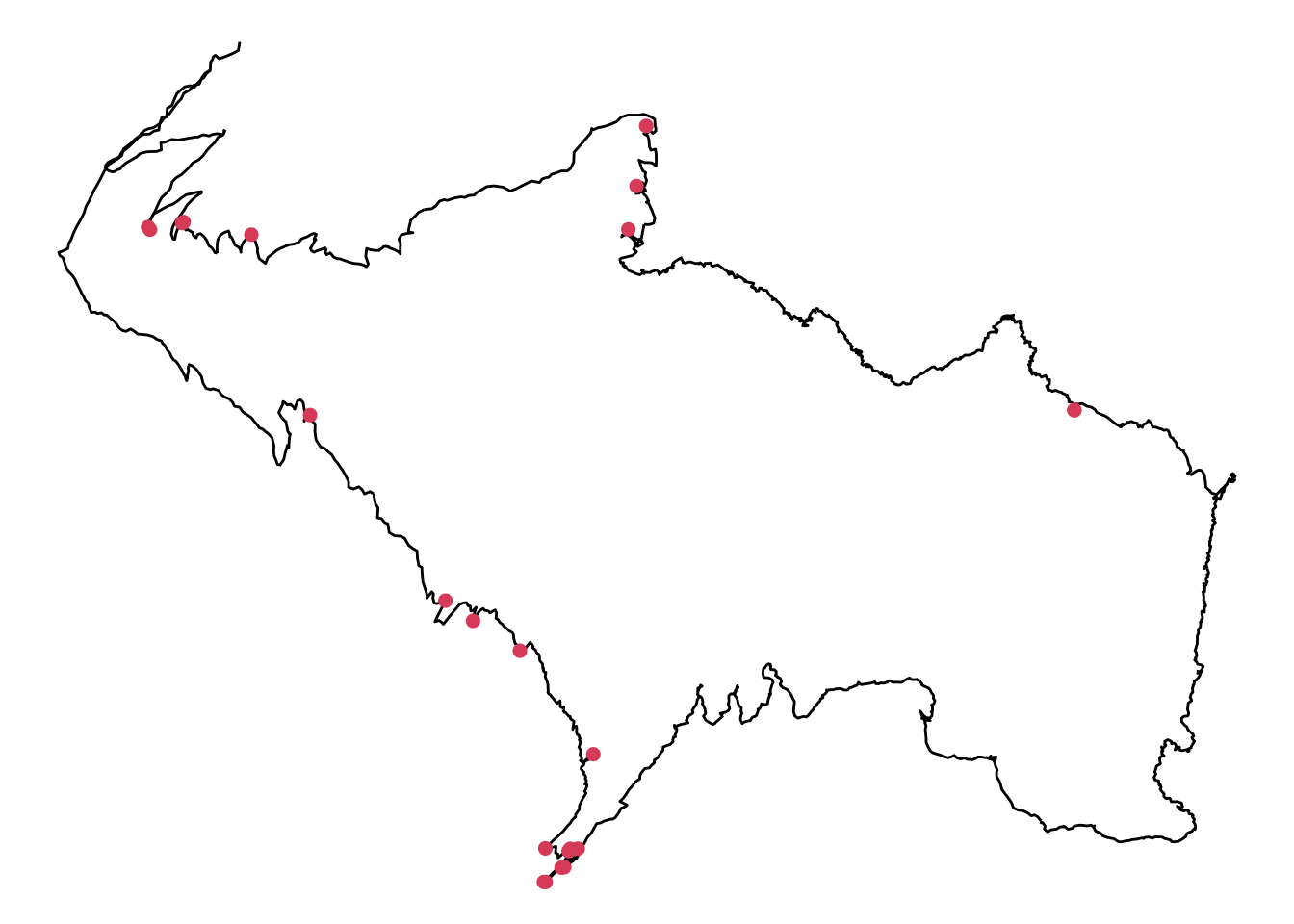
Le choix du seuil est primordial, puisqu’il peut influencer grandement le nombre de points outlier. Il s’agit donc de le choisir avec parcimonie, en regardant attentivement la distribution seuil~nombre de points dans un histogramme. Les outliers peuvent influencer les résultats finaux d’une trace GPS : vitesse, distance, accélération. Il est donc impotant de savoir les gérer.